Estadístico de prueba para una media

Si se quiere probar las hipótesis

Bilateral	Unilateral
\left\{\begin{matrix} H_0: \mu = \mu_0\\ H_a: \mu \neq \mu_0 \end{matrix}\right.	\left\{\begin{matrix} H_0: \mu = \mu_0\\ H_a: \mu > \mu_0 \end{matrix}\right.	\left\{\begin{matrix} H_0: \mu = \mu_0\\ H_a: \mu < \mu_0 \end{matrix}\right.

En una muestra de tamaño n, con desviación estándar S, y media muestral x̅, el estadístico de prueba es

t_0 = \frac{\bar{x}-\mu_0}{S/\sqrt{n}}

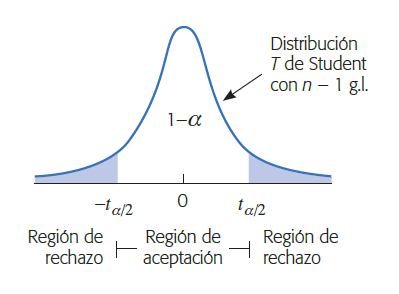
Si H₀ se cumple entonces dicho estadístico se distribuye T de Student con n-1 grados de libertad. H₀ se rechaza si el valor absoluto del estadístico de prueba es mayor al valor crítico, es decir

|t_0| > t_{\alpha / 2, n-1}	t_0 > t_{\alpha, n-1}	t_0 < -t_{\alpha, n-1}
Para pruebas bilaterales	Para pruebas unilaterales

Regiones de rechazo y de aceptación para hipótesis bilateral

Estadístico de prueba para la diferencia de medias - supuesto de varianzas iguales

Si se quiere probar las hipótesis

Bilateral	Unilateral
\left\{\begin{matrix} H_0: \mu_1 = \mu_2\\ H_a: \mu_1 \neq \mu_2 \end{matrix}\right.	\left\{\begin{matrix} H_0: \mu_1 = \mu_2\\ H_a: \mu_1 > \mu_2 \end{matrix}\right.	\left\{\begin{matrix} H_0: \mu_1 = \mu_2\\ H_a: \mu_1 < \mu_2 \end{matrix}\right.

En dos muestras aleatorias de tamaño n₁ y n₂, con desviación estándar S₁ y S₂, y medias muestrales x̅₁ y x̅₂, respectivamente, y que además cumplen con el supuesto de varianzas iguales, el estadístico de prueba es

t_0 = \frac{ \bar{x}_1 - \bar{x}_2 } {S_p \sqrt{\frac{1}{n_{x_1}} + \frac{1}{n_{x_2}} } }

donde 

S_p^{2}=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}

Si H₀ se cumple entonces dicho estadístico se distribuye T de Student con n₁+n₂-2 grados de libertad. H₀ se rechaza si el valor absoluto del estadístico de prueba es mayor al valor crítico, es decir

|t_0| > t_{\alpha/2, n_1+n_2-2}	t_0 > t_{\alpha, n_1+n_2-2}	t_0 < -t_{\alpha, n_1+n_2-2}
Para pruebas bilaterales	Para pruebas unilaterales

Estadístico de prueba para la diferencia de medias - supuesto de varianzas desiguales

Si se quiere probar las hipótesis

Bilateral	Unilateral
\left\{\begin{matrix} H_0: \mu_1 = \mu_2\\ H_a: \mu_1 \neq \mu_2 \end{matrix}\right.	\left\{\begin{matrix} H_0: \mu_1 = \mu_2\\ H_a: \mu_1 > \mu_2 \end{matrix}\right.	\left\{\begin{matrix} H_0: \mu_1 = \mu_2\\ H_a: \mu_1 < \mu_2 \end{matrix}\right.

En dos muestras aleatorias de tamaño n₁ y n₂, con desviación estándar S₁ y S₂, y medias muestrales x̅₁ y x̅₂, respectivamente, y que además cumplen con el supuesto de varianzas desiguales, el estadístico de prueba es

 

t_0 = \frac{ \bar{x}_1 - \bar{x}_2 } { \sqrt{\frac{S_1}{n_{x_1}} + \frac{S_2}{n_{x_2}} } }

Si H₀ se cumple entonces dicho estadístico se distribuye T de Student con ν grados de libertad, donde

\nu = \frac{\left ( \frac{S^2_1}{n_1}+\frac{S^2_2}{n_2}\right )^2}{\frac{(S_1^2/n_1)^2}{n_1+1}+\frac{(S_2^2/n_2)^2}{n_2+1}}-2

H0 se rechaza si el valor absoluto del estadístico de prueba es mayor al valor crítico, es decir

|t_0| > t_{\alpha/2, \nu}	t_0 > t_{\alpha, \nu}	t_0 < -t_{\alpha, \nu}
Para pruebas bilaterales	Para pruebas unilaterales